Question

Consider the function ​f(x)equalscosine left parenthesis x squared right parenthesis. a. Differentiate the Taylor series about 0 for​ f(x). b. Identify the function represented by the differentiated series. c. Give the interval of convergence of the power series for the derivative.

Answer 1

I suppose you mean

`f(x)=\cos(x^2)`

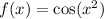
Recall that

`\cos x=\displaystyle\sum_(n=0)^\infty(-1)^n(x^(2n))/((2n)!)`

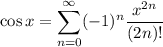
which converges everywhere. Then by substitution,

`\cos(x^2)=\displaystyle\sum_(n=0)^\infty(-1)^n((x^2)^(2n))/((2n)!)=\sum_(n=0)^\infty(-1)^n(x^(4n))/((2n)!)`

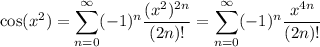
which also converges everywhere (and we can confirm this via the ratio test, for instance).

a. Differentiating the Taylor series gives

`f'(x)=\displaystyle4\sum_(n=1)^\infty(-1)^n(nx^(4n-1))/((2n)!)`

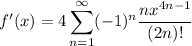
(starting at
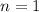`n=1` because the summand is 0 when
`n=0`)

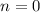b. Naturally, the differentiated series represents

`f'(x)=-2x\sin(x^2)`

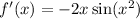
To see this, recalling the series for
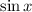`\sin x`, we know

`\sin(x^2)=\displaystyle\sum_(n=0)^\infty(-1)^(n-1)(x^(4n+2))/((2n+1)!)`

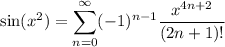
Multiplying by
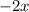`-2x` gives

`-x\sin(x^2)=\displaystyle2x\sum_(n=0)^\infty(-1)^n(x^(4n))/((2n+1)!)`

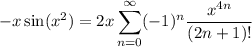
and from here,

`-2x\sin(x^2)=\displaystyle 2x\sum_(n=0)^\infty(-1)^n(2nx^(4n))/((2n)(2n+1)!)`

`-2x\sin(x^2)=\displaystyle 4x\sum_(n=0)^\infty(-1)^n(nx^(4n))/((2n)!)=f'(x)`

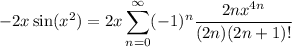
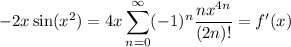
c. This series also converges everywhere. By the ratio test, the series converges if

`\displaystyle\lim_(n\to\infty)\left|((-1)^(n+1)((n+1)x^(4(n+1)))/((2(n+1))!))/((-1)^n(nx^(4n))/((2n)!))\right|=|x|\lim_(n\to\infty)\frac{(n+1)/((2n+2)!)}{\frac n{(2n)!}}=|x|\lim_(n\to\infty)(n+1)/(n(2n+2)(2n+1))<1`

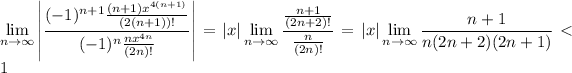
The limit is 0, so any choice of
`x` satisfies the convergence condition.