Answer:
The moment of inertia of disc about own axis is 1 kg-m².
Step-by-step explanation:
Given that,
Mass of ring m= 1 kg
Moment of inertia of ring at diameter
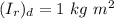
The radius of metallic ring and uniform disc both are equal.
So,
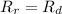
We need to calculate the value of radius of ring and disc
Using theorem of perpendicular axes
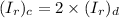
Put the value into the formula
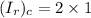

Put the value of moment of inertia
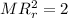
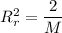
Put the value of M
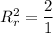
So,
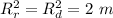
We need to calculate the moment of inertia of disc about own axis
Using formula of moment of inertia
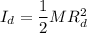
Put the value into the formula
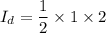
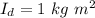
Hence, The moment of inertia of disc about own axis is 1 kg-m².