Question

What are the roots of x in -10x2 + 12x - 9 = 0?

Answer 1

29/12

Explanation:

-20+12x-9=0

-29+12×=0

12x=29

x=29/12

Answer 2

The roots of the equation
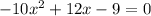`\( -10x^2 + 12x - 9 = 0 \)` are complex numbers and can be expressed as:

`\[ x = (12 \pm 6i√(6))/(-20) \]`

`\[ x = (6 \pm 3i√(6))/(-10) \]`

How to get the roots of the equation

In your equation, a = -10, b = 12, and c = -9. Plugging these values into the formula, we get:

`\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]`

a = -10 , b = 12, and c = -9 . Now, substitute these values into the quadratic formula:

`\[ x = (-12 \pm √((12)^2 - 4(-10)(-9)))/(2(-10)) \]`

Simplify inside the square root:

`\[ x = (-12 \pm √(144 - 360))/(-20) \]`

`\[ x = (-12 \pm √(-216))/(-20) \]`

The square root of -216 is \
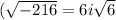`( √(-216) = 6i√(6) \)` (where ( i ) is the imaginary unit).

Therefore, the roots of the equation
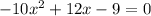`\( -10x^2 + 12x - 9 = 0 \)` are complex numbers and can be expressed as:

`\[ x = (12 \pm 6i√(6))/(-20) \]`

`\[ x = (6 \pm 3i√(6))/(-10) \]`