Answer:
See graph
Explanation:
Let p(x) be the polynomial.
Since -6 is a root with multiplicity 3,
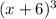 is a factor of p(x).
is a factor of p(x).
Since 2 is a root with multiplicity 4,
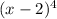 is a factor of p(x).
is a factor of p(x).
This implies that:
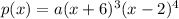
Since a<0, and the degree of the polynomial is odd(4+3=7), the graph falls on the left and also falls to the right.
In other words, the graph approaches positive infinity on the left an negative infinity on the right.
See attachment.