Question

In a survey of 1005 ​adults, a polling agency​ asked, "When you​ retire, do you think you will have enough money to live comfortably or not. Of the 1005 ​surveyed, 531 stated that they were worried about having enough money to live comfortably in retirement. Construct a 90​% confidence interval for the proportion of adults who are worried about having enough money to live comfortably in retirement

Answer 1

Answer: (0.504, 0.556)

Explanation:

Given : Sample size : n= 1005

Number of adults stated that they were worried about having enough money to live comfortably in retirement = 531

Then the proportion of adults stated that they were worried about having enough money to live comfortably in retirement :
`p=(531)/(1005)\approx0.53`

Significance level :
`\alpha: 1-0.90=0.1`

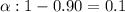
Critical value :
`z_(\alpha/2)=1.645`

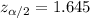
The confidence interval for population proportion is given by :-

`p\pm\ z_(\alpha/2)\sqrt{(p(1-p))/(n)}\\\\=0.53\pm(1.645)\sqrt{(0.53(1-0.53))/(1005)}\\\\\approx0.53\pm0.026\\\\=(0.504,\ 0.556)`

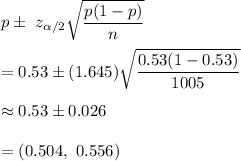
Hence, the 90​% confidence interval for the proportion of adults who are worried about having enough money to live comfortably in retirement = (0.504, 0.556)