Question

In the population, “intelligence quotient” scores (IQ’s) are approximately normally distributed with a mean of 100 and a standard deviation of 15. Suppose we plan to obtain IQ scores of a random sample of n = 30 individuals, and then we’ll compute the sample mean and sample standard deviation. Suppose you were unsure of the value of the population standard deviation, and so you plan to use only the sample standard deviation. Find the exact probability that the sample mean will be within one-third of one sample standard deviation of the population mean.

Answer 1

prob= 0.326

Explanation:

Given that IQ scores (X) are normal (100, 15)

n = sample size =30

If we do not know population std deviation we can use t critical values with df =29

Std error of sample =
`(15)/(√(30) ) \\=2.7387`

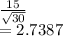
Thus we have sample mean is having mean = 100 and std dev = 2.7387

Mean falls within 1 std dev means mean lies in the interval

=100±2.7387

=(97.2613, 102.7387)

Prob t lies between -1 and 1 is 0.326