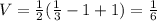Question

Find the volume of the wedge with vertices at points (0,0,0), (1,0,0), (0,1,0), (0,0,1) by integrating the area of cross-sections parallel to the yz-plane. *

Answer 1

V = 1/6 cubic units

Explanation:

Applying the concept of integrals for volume calculation:

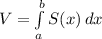`V = \int\limits^b_a {S(x)} \, dx` (1)

V = volume of the solid bounded by x = a and x = b

S(x) = cross section area of the solid, perpendicular to the x axis

From the figure we have that S is the area of a triangle that has base Z and height Y

Area of the triangle =
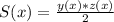`S(x)=(y(x)*z(x))/(2)` (2)

Calculation of y(x) and z(x)

We apply the equation of the point-slope line (plane xy):

Slope =
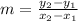`m = (y_(2) - y_(1) )/(x_(2) - x_(1))` (3)

Equation of the line =
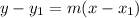`y - y_(1) =m(x-x_(1) )` (4)

Replacing the points (1,0) and (0,1) in (3):

`m=(1-0)/(0-1) =-1`

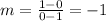
Replacing the point (1,0) and m = -1 in (4):

`y-0=(-1)(x-1)`

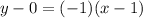
y(x) = -x + 1 (Line A-B) (5)

We apply the equation of the point-slope line (plane xz):

Slope =
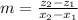`m = (z_(2) - z_(1) )/(x_(2) - x_(1))` (6)

Equation of the line =
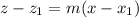`z - z_(1) =m(x-x_(1) )` (7)

Replacing the points (1,0) and (0,1) in (6):

`m=(1-0)/(0-1) =-1`

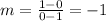
Replacing the point (1,0) and m = -1 in (7):

`z-0=(-1)(x-1)`

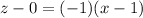
z(x) = -x + 1 (Line A-C) (8)

Replacing (5) and (8) in (2)

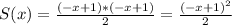`S(x) = ((-x + 1) * (-x + 1))/(2) =((-x + 1)^(2) )/(2)` (9)

Replacing (9) in (1) and knowing that a = 0 and b = 1:

`V = \int\limits^1_0 {((-x + 1)^(2) )/(2)} \, dx = \int\limits^1_0 {(x^(2)-2x+1 )/(2)} \, dx`

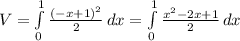
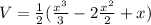`V =(1)/(2) ((x^(3) )/(3) -2(x^(2) )/(2) +x)` evaluated from x=0 to x=1

`V= (1)/(2) ((1)/(3) -1 +1) = (1)/(6)`