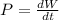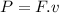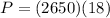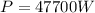Answer:
Part a)
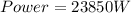
Part b)
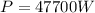
Step-by-step explanation:
Part a)
As we know that the acceleration of the object is given as rate of change in velocity
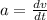
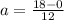
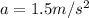
now we know that
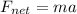
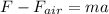


now the work done by the engine
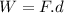
here distance covered by the engine is given as
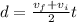

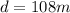
now we have
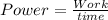
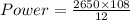
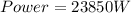
Part b)
Instantaneous power is given as