Answer: The concentration of
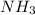 required will be 0.285 M.
required will be 0.285 M.
Step-by-step explanation:
To calculate the molarity of
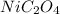 , we use the equation:
, we use the equation:
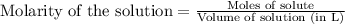
Moles of
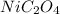 = 0.016 moles
= 0.016 moles
Volume of solution = 1 L
Putting values in above equation, we get:
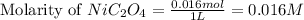
For the given chemical equations:
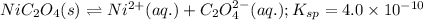
![Ni^(2+)(aq.)+6NH_3(aq.)\rightleftharpoons [Ni(NH_3)_6]^(2+)+C_2O_4^(2-)(aq.);K_f=1.2* 10^9](https://img.qammunity.org/2020/formulas/chemistry/high-school/my601w73gyf3if368kwlxad9w8jlfgbmaf.png)
Net equation:
![NiC_2O_4(s)+6NH_3(aq.)\rightleftharpoons [Ni(NH_3)_6]^(2+)+C_2O_4^(2-)(aq.);K=?](https://img.qammunity.org/2020/formulas/chemistry/high-school/thtumrsnckkg1s6jucs3e1herkk5ez71g2.png)
To calculate the equilibrium constant, K for above equation, we get:
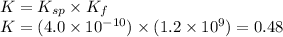
The expression for equilibrium constant of above equation is:
![K=([C_2O_4^(2-)][[Ni(NH_3)_6]^(2+)])/([NiC_2O_4][NH_3]^6)](https://img.qammunity.org/2020/formulas/chemistry/high-school/ake1cypmnkimpn8pjf01x9442kon97fs2x.png)
As,
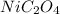 is a solid, so its activity is taken as 1 and so for
is a solid, so its activity is taken as 1 and so for
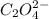
We are given:
![[[Ni(NH_3)_6]^(2+)]=0.016M](https://img.qammunity.org/2020/formulas/chemistry/high-school/u4clist9zpxtzk31n6mo9z7dx2djruttp6.png)
Putting values in above equations, we get:
![0.48=(0.016)/([NH_3]^6)}](https://img.qammunity.org/2020/formulas/chemistry/high-school/dvfuq8akd8zom0531oaa1vitho4j0cgkp3.png)
![[NH_3]=0.285M](https://img.qammunity.org/2020/formulas/chemistry/high-school/e9mbjv0ccbektsomoexlt1idtv34nyqvdu.png)
Hence, the concentration of
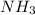 required will be 0.285 M.
required will be 0.285 M.