Question

A padlock for your gym locker uses a three number sequence to open the lock. if the numbers go from 1 to 28, how many different sequences are on the dial without repeating a number?

Answer 1

19,656

Explanation:

Numbers used in locker = 3

Total numbers available = 28

Repetition is not allowed, so one number can be used only once. The order of number matters in the locker e.g. 123 password is not the same as 231. Since, the order of numbers matter, this is a problem of permutations. We need to find the number of different sequences formed with 28 numbers taken 3 at a time. This can be represented as 28P3

The formula for permutations is:

`^(n)P_(r)=(n!)/((n-r)!)`

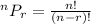
For the given case, we will have:

`^(28)P_(3)=(28!)/((28-3)!)\\\\ = (28!)/(25!)\\\\ = 19656`

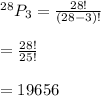
This means, 19,656 different 3 numbered sequences are possible for the locker.