Question

A coffee dispensing machine is supposed to deliver eight ounces of liquid into each paper cup, but a consumer believes that the actual mean amount is less. The consumer obtained a sample of 49 cups of the dispensed liquid with an average of 7.75 ounces. If the sample variance of the dispensed liquid delivered per cup is 0.81 ounces, and α = 0.05, the appropriate decision is ________.

Answer 1

Answer: reject the 8 ounce claim

Explanation:

Answer 2

Answer: We have enough evidence to support the consumer's claim that the actual mean amount is less.

Explanation:

Let
`\mu` represents the population mean for the dispensed liquid into each paper cup.

According to the claim , we have the following set of hypothesis :-

`H_0 : \mu=8\\\\ H_1: \mu<8`

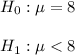
Since the alternative hypothesis is left-tailed , so the hypothesis test is left tailed test.

For sample , we have

Sample size : n=49 , which is large (n>30) , so we use z-test.

Sample mean :
`\overline{x}=7.75`

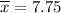
Standard deviation :
`\sigma= √(0.81)=0.9`

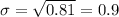
The test statistic for population mean is given by :-

`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}\\\\\Rightarrow\ z=(7.75-8)/((0.9)/(√(49)))\\\\\Rightarrow\ z\approx-1.94`

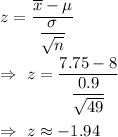
The p-value =
`P(z<-1.94)=0.0261898`

Since , the p-value is less than the significance level (0.05), so we reject the null hypothesis .

Thus , we conclude that we have enough evidence to support the alternative hypothesis i.e. the actual mean amount is less.