Question

Surface roughness can be measured as either an arithmetic average (AA) or a root-mean-square (RMS) average. Which value is almost always greater for most surfaces?

Answer 1

Root-mean-square (RMS)

Explanation:

Arithmetic average is the average of all the values of the surface peaks and valleys.

`AA=(\sum^n_(i=1)|y_i|)/(n)`

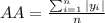
Root mean square is the root of the sum of the squares of each of the values of the surface peaks and valleys divided by the number of values

`RMS=\sqrt{\frac{\sum^n_(i=1){y_i}^2}{n}}`

where n = the number of values

So, the root-mean-square RMS is always greater than the arithmetic average (AA).