Answer:
The graph in the attached figure
Explanation:
we have
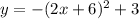
Factor the leading coefficient
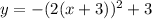
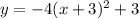
This is the equation of a vertical parabola in vertex form
The parabola open downward
The vertex is a maximum
The vertex is the point (-3,3)
Find out the x-intercepts (values of x when the value of y is equal to zero)
For y=0
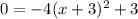
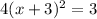
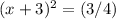
square root both sides
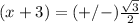
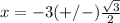
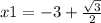 ----->
----->
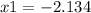
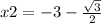 ----->
----->
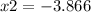
using a graphing tool
The graph in the attached figure