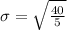Question

Compute the standard deviation for the set of data.

2, 4, 6, 8, 10

a.2.83

c.6.32

b.8

d.64

Answer 1

Answer: Option a

`\sigma=2.83`

Explanation:

The formula for calculating the standard sigma deviation is:

`\sigma=\sqrt{\frac{\sum_(i=1)^n(X_i-{\displaystyle {\overline {x}}})^2}{N}}`

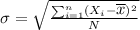
Where

`{\displaystyle {\overline {x}}}` is the average

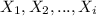`X_1, X_2, ..., X_i` is the data set

N is the amount of data

First we calculate the average

`{\displaystyle {\overline {x}}}=(2+4+6+8+10)/(5)`

`{\displaystyle {\overline {x}}}=6`

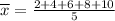
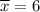
Now we calculate the square differences

`(2-6)^2=16\\\\(4-6)^2=4\\\\(6-6)^2=0\\\\(8-6)^2=4\\\\(10-6)^2=16`

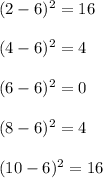
Then

`\sum(X_i-{\displaystyle {\overline {x}}})^2} = 16+ 4+0+4+16=40`

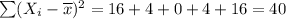
Finally the standard deviation for the set of data is:

`\sigma=\sqrt{(40)/(5)}`

`\sigma=2.83`