Question

Seven Eleven Stores is planning an expansion project that it desires to finance with newly issued preferred stock. The firm has an outstanding issue of preferred stock that pays a dividend of $4.25 per share, which is trading for $65 per share. The investment bankers have advised Seven Eleven that flotation costs will be 8% per share. What will be the cost of the newly issued preferred shares? 1. 8.3% 2. 7.1% 3. 9.7% 4. 6.5%

Answer 1

2. 7.1%

Step-by-step explanation:

We use the formula to calculate the return of the Gordon Model:

`(divends)/(return-growth) = Intrinsic \: Value`

`(divends)/(Price) = $return - growth`

`(divends)/(Price) +growth = return`

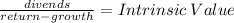
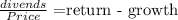
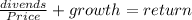
Because the issue of new share has a flotation cost, it must be discount from the share price, giving us the final formula:

`$Cost of Equity =(D_1)/(P(1-f)) +g`

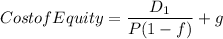
D1 4.25

P 65

f $0.08

g 0 (there is no growth stimated so we assume zero)

`$Cost of Equity =(4.25)/(65(1-0.08)) +0`

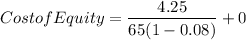
Ke 0.071070234

Ke = 7.1070% = 7.1%