Answer:
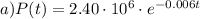
Step-by-step explanation:
(a)
With the given information remember that the exponential model for the population of the country is given by
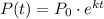
where
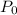 is the initial population and
is the initial population and
 is the proportionality constant for the problem. In our case we know that k=-0.006, but we don't know the value of
is the proportionality constant for the problem. In our case we know that k=-0.006, but we don't know the value of
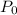 . To find the initial population, we must take into account that we are letting t=0 correspond to the year 2000, hence t=7 correspnds to the year 2007, and we know that
. To find the initial population, we must take into account that we are letting t=0 correspond to the year 2000, hence t=7 correspnds to the year 2007, and we know that
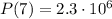 . Using the model, we get that
. Using the model, we get that
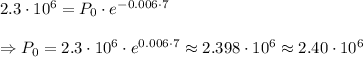
(b) To predict the population of the country in the year 2022, note that t=22 corresponds to this year. Hence, the population of the country in 2022 would be
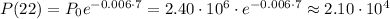
arround 2.10 millions.