Question

The temperature at pointâ (x,y) on a metal plate is Upper T left parenthesis x comma y right parenthesis equals 144 x squared minus 144 xy plus 36 y squared. An ant on the plate walks around the circle of radius 5 centered at the origin. What are the highest and lowest temperatures encountered by theâ ant?

Answer 1

Highest: 4500

Lowest: 0

Step-by-step explanation:

The temperature function in the metal plate is:

`T(x,y)=144x^2-144xy+36y^2`

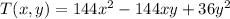
It can be factorized as:

`T(x,y)=(12x-6y)^2`

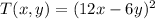
Additionally, the ant walks through the circle of radius 5 centered at the origin, which equation is:

`x^2+y^2=25`

In order to find the temperature through the path of the ant, it is necessary to substitute the path equation in the temperature function:

`y^2=25-x^2\\y=√(25-x^2)\\T(x)=(12x-6√(25-x^2))^2`

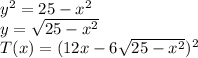
This last equation is the equation of the temperature profile just across the path of the ant, because it is like the equation "were said" that
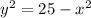`y^2=25-x^2`, so it is just for the circle of radius 5.

We are going to apply the first derivative criteria in order to find the maximum and minimum values for the temperature. The criteria consist in finding the values for x that satisfy:

`(dT)/(dx)=0`

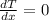
So, let's derive the temperature function:

First, apply the power rule:

`T(x)=(12x-6√(25-x^2))^2\\(dT)/(dx)=2*(12x-6√(25-x^2))*(d)/(dx) (12x-6√(25-x^2))`

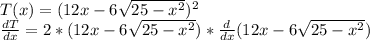
The, apply the sum rule:

`(dT)/(dx)=2*(12x-6√(25-x^2))*((d)/(dx) 12x-(d)/(dx)6√(25-x^2))\\(dT)/(dx)=2*(12x-6√(25-x^2))*(12-6(d)/(dx)(25-x^2)^{(1)/(2)} )`

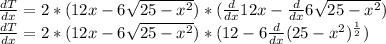
And the power rule again (Remember to always apply the chain rule as we show you):

`(dT)/(dx)=2*(12x-6√(25-x^2))*(12-6*(1)/(2) (25-x^2)^{(-1)/(2)}(d)/(dx)(25-x^2))\\(dT)/(dx)=2*(12x-6√(25-x^2))*(12-6*(1)/(2) (25-x^2)^{(-1)/(2)}*-2x)\\(dT)/(dx)=2*(12x-6√(25-x^2))*(12+6x(25-x^2)^{(-1)/(2)})`

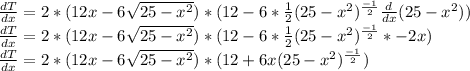
Then, we are going to equal the derivative to zero and solve the equation:

`2*(12x-6√(25-x^2))*(12+6x(25-x^2)^{(-1)/(2)})=0`

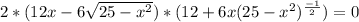
As we have a product of two expressions, the total left side of the equation will be zero if one of the multipliers is zero, so, we have two equations:

`(12x-6√(25-x^2))=0`

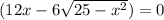
and

`(12+6x(25-x^2)^{(-1)/(2)})=0`

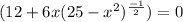
Let's try with the first:

`(12x-6√(25-x^2))=0\\12x=6√(25-x^2)\\2x=√(25-x^2)\\4x^2=25-x^2\\5x^2=25\\x^2=5\\x=\pm √(5)`

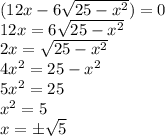
Let's continue with the other:

`12+6x(25-x^2)^{(-1)/(2)}=0\\12+\frac{6x}{(25-x^2)^{(1)/(2)}}=0\\\frac{6x}{(25-x^2)^{(1)/(2)}}=-12\\6x=-12(25-x^2)^{(1)/(2)}\\x=-2(25-x^2)^{(1)/(2)}\\x^2=4(25-x^2)\\x^2=100-4x^2\\5x^2=100\\x^2=20\\x=\pm √(20)=\pm 2√(5)`

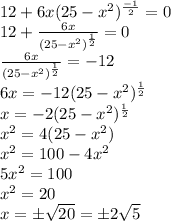
Now we have four possible values for x:
`√(5),- √(5),2√(5),-2√(5)`

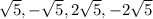
Then, we can evaluate the temperature function:

`T(x)=(12x-6√(25-x^2))^2`

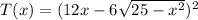
in order to find which of these values are the highest and the ones that are the lowest.

For
`x=√(5)` and
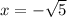`x=-√(5)`, the temperature founded is zero (Another intermediate temperature is found if we consider the negative root in
`√(25-x^2)`, but it is not the lowest either the highest).

For
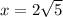`x=2√(5)` and
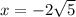`x=-2√(5)` the temperature founded is 4500. Again, intermediate values can be found considering the negative root in
`√(25-x^2)`, but they are not the lowest either the highest.