Question

Sandra wants to rent a car to take a trip and has a budget of $90. There is a fixed rental fee of $30 and a daily fee of $10. Write an inequality that would be used to solve for the maximum number of days for which Sandra can rent the car on her budget.

Answer 1

The maximum number of days Sandra can rent the car on her budget is 6.

Step-by-step explanation:

To solve for the maximum number of days Sandra can rent the car on her budget, we need to set up an inequality. Let the number of days be represented by d. The total cost (C) of renting the car for d days can be calculated by adding the fixed rental fee ($30) to the product of the daily fee ($10) and the number of days (d). So the inequality would be:

30 + 10d ≤ 90

To solve for d, subtract 30 from both sides of the inequality:

10d ≤ 60

Then divide both sides by 10:

d ≤ 6

So, the maximum number of days Sandra can rent the car on her budget is 6.

Answer 2

The maximum number of days for which Sandra can rent the car on her budget is 6.

Step-by-step explanation:

Let n be the number of of days for which Sandra can rent the car on her budget.

Fixed rent = $30

Daily fee for 1 day = $10

Daily fee for n days = 10n

So, Total fees = 30+10n

Sandra's budget is $90 .

She cannot spend more than $90.

So, inequality becomes :
`30+10n\leq 90`

`10n\leq 90-30`

`10n\leq 60`

`n\leq 6`

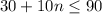
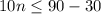
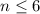
So, the maximum number of days for which Sandra can rent the car on her budget is 6.