Step-by-step explanation:
The speed of sound in copper,
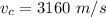
The speed of sound in air at 1.34°C,
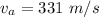
The sound of the blow, traveling through air, reaches the opposite end of the rod 3.18 ms later than the sound transmitted through the rod. Time difference,
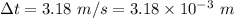
Since,

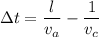
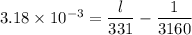
l = 1.17 meters
So, the length of the rod is 1.17 meters. Hence, this is the required solution.