Answer: The lines WX and YZ are parallel.
Step-by-step explanation: We are given to check whether the lines WX and YZ are parallel, perpendicular or neither if the co-ordinates of the endpoints of both the lines are
W(3,4), X(5,7), Y(8,2) and Z(6,-1).
We know that the slope of a straight line passing through the points (a, b) and (c, d) is given by
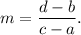
So, the slope of the line WX is
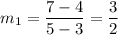
and the slope of line YZ is
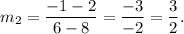
Since, we get
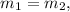 so the two lines WX and YZ are parallel.
so the two lines WX and YZ are parallel.
Thus, the lines WX and YZ are parallel.