Question

Let x be a real number. Find the lowest possible value of |5x^2 - 16| + |10x - 2|.

Note: | | refers to absolute value.​

Answer 1

15.8

Explanation:

`x \in \mathbb{R}`

`|5x^2 - 16| + |10x - 2|`

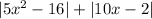
Once we are working with absolute values, the expression will always be positive, therefore, to get the lowest value for the expression, the lowest value for x should be 0.

`|5(0)^2 - 16| + |10(0) - 2|`

`|- 16| + |- 2|`

`16 + 2`

`18`

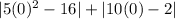
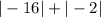
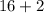
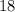
But this is not the right approach and this is not the lowest value. For this question, you may think that

`|5x^2 - 16| + |10x - 2|>0`

For

`|5x^2 - 16| + |10x - 2|=0, \\exists x \in \math{R}`

Therefore,

`|5x^2 - 16| + |10x - 2|>0`

Solving that

`$|5x^2-16| \implies \left|5\left(-(4)/(√(5))\right)^2-16\right| = 0$`

`$|10x - 2| \implies \left|10\left((1)/(5) \right) - 2\right| =0$`

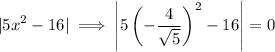
Once it is true for all values of x in the Real set, it means the intervals,

`$x\le -(4)/(√(5))$`

`$-(4)/(√(5))<x<(1)/(5)$`

`$(1)/(5)\le x<(4)/(√(5))$`

`$x\ge (4)/(√(5))$`

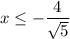
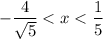
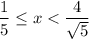
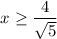
Are true and equal to
`x\in(-\infty, \infty)`

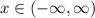
The lowest value for
`x` will be

`$(4)/(√(5) ) \text{ or } (1)/(5) $`

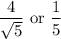
If you replace one of these values for
`x`, you will find that
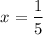`$x=(1)/(5) $` is the value that will give the lowest value for the expression.

`$\left|5\left((1)/(5)\right)^2-16\right| + \left|10\left((1)/(5) \right) - 2\right| = 15.8$`