Question

What is the quadratic. Formula?

Answer 1

`x = \frac{ - b ± \sqrt{ {b }^(2) - 4ac } }{2a}`

Explanation:

For example, we'll use this quadratic equation.

`{x}^(2) + 5x + 6`

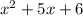
To understand how to plug it into the formula we need to know what each term represents.

`a {x}^(2) + bx + c`

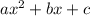
So the equation above would be put into the formula like this.

`x = \frac{ - 5± \sqrt{ {5}^(2) - 4(1)(6) } }{2(1)}`

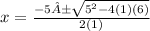
Then we would solve

`( - 5± √(25 - 24) )/(2) \\ \\ = ( -5±1)/(2)`

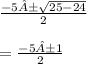
Now, the equation will branch off into one that solves when addition and one when subtraction.

`( - 5 + 1)/(2) = ( - 4)/(2) = - 2 \\ \\ ( - 5 - 1)/(2) = ( - 6)/(2) = - 3`

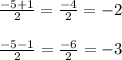
So x={-3, -2} (-3 and -2)