Question

A set of tires is designed to last 6 years, with a standard deviation of 2 years. What is the probability that a tire will last less than 4 years?

1%
10%
16%
26%

Answer 1

16%.

Explanation:

We may assume that the times are normally distributed.

We first find the z-score which is the (value - mean) / standard deviation.

z-score = (4 - 6)/2 = -1.

Looking up the value for -1 on a z-score normal distribution table we find that -1 gives us 0.1587 - that is 16%.

Answer 2

Answer: 16%

Explanation:

Let the mean of the population of tires denoted by
`\mu` and standard deviation as
`\sigma`.

Given : A set of tires is designed to last 6 years, with a standard deviation of 2 years.

i.e.
`\mu=6` and
`\sigma=2`

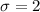
Let x be the random variable that represents the life of tires.

Z-score :
`(x-\mu)/(\sigma)`

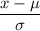
For x = 4 , we have

`(4-6)/(2)=-1`

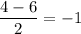
Now by using standard normal distribution table we have,

The probability that a tire will last less than 4 years will be :-

`P(x<4)=P(z<-1)= 0.1586553\approx0.16=16\%`

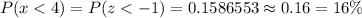
Hence, the probability that a tire will last less than 4 years = 16%