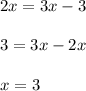Question

See the attachment below for the question.

Answer 1

Answer: Third option.

Explanation:

We need to remember that:

`a^m=a^n\\\\m=n`

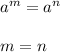
In this case, given this expression:

`4^x`
`=8^(( x- 1))`

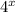
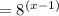
We need to descompose 4 and 8 into their prime factors:

`4=2*2=2^2`

`8=2*2*2=2^3`

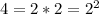
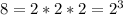
Rewriting the expression:

`2^(2x)`
`=2^(3(x - 1) )`

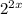
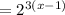
Then:

`2x = 3(x - 1)`

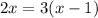
Finally, applying Distributive property on the right side and solving for "x", we get:

`2x=3x-3\\\\3=3x-2x\\\\x=3`

Answer 2

The correct answer is third option

x = 3

Explanation:

It is given that,

4ˣ = 8⁽ˣ ⁻ ¹⁾

To find the value of x

4ˣ = (2²)ˣ

8⁽ˣ ⁻ ¹⁾ = (2³)⁽ˣ ⁻ ¹⁾

4ˣ = 8⁽ˣ ⁻ ¹⁾

(2²)ˣ = (2³)⁽ˣ ⁻ ¹⁾

2²ˣ = 2⁽³ˣ ⁻ ³⁾

2x = 3x - 3

3x - 2x = 3

x = 3

The correct answer is third option

x = 3