Answer:
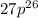
Explanation:
Let's start defining some properties about exponents.
In the properties, we use a,b,c where a,b,c ∈ IR.
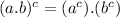 (I)
(I)
This means, that we can distribute the exponent respect a multiplication.
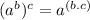 (II)
(II)
And finally
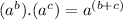 (III)
(III)
Using this three properties we are going to solve the exercise :
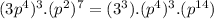
We used properties (I) and (II)
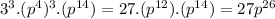
The final step is to use property (II) again and the property (III)