Answer:
Explanation:
Given a series
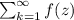 , the Weierstrass M-test tell us that if we find a sequence of positive numbers
, the Weierstrass M-test tell us that if we find a sequence of positive numbers
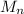 such that
such that
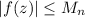 in a certain domain D, and the series
in a certain domain D, and the series
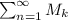 converges, then the series
converges, then the series
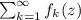 converges uniformly in the domain D.
converges uniformly in the domain D.
So, our objective is to find the so called sequence
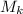 . The main idea is to bound the sequence of functions
. The main idea is to bound the sequence of functions
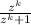 .
.
Now, notice that the values of z are always positive, so
 is always positive, so
is always positive, so
 for all values of z in
for all values of z in
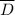 . Then,
. Then,
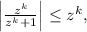
because if we make the values of the denominator smaller, the whole fraction becomes larger.
Moreover, as z is in the interval [0,r], we have that
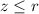 and as consequence
and as consequence
 . With this in addition to the previous bound we obtain
. With this in addition to the previous bound we obtain
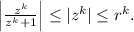
With this, our sequence is
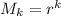 and the corresponding series is
and the corresponding series is
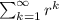 , which is a geometric series with ratio less than 1, hence it is convergent.
, which is a geometric series with ratio less than 1, hence it is convergent.
Then, as consequence of Weierstrass M-test we have the uniform convergence of the series in the given domain.