Question

A student and his lab partner create a single slit by carefully aligning two razor blades to a separation of 0.530 mm. When a helium–neon laser at 543 nm illuminates the slit, a diffraction pattern is observed on a screen 1.55 m beyond the slit. Calculate the angle θdark to the first minimum in the diffraction pattern and the width of the central maximum.

Answer 1

angle = 0.058699 degree

width of central maximum is 3.170566 ×
`10^(-3) )  m</strong></p><p><strong>Explanation:</strong></p><p>Given data </p><p>separation d = 0.530 mm = 0.530×[tex]10^(-3)` m

distance D = 1.55 m

wavelength w = 543 nm = 543×
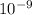`10^(-9)` m

to find out

angle θ and width of the central maximum

solution

we know according to first condition first dark that mean

wavelength = dsinθ

so put value and find θ

543×
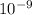`10^(-9)` = 0.530×
`10^(-3)` ×sinθ

sinθ = 543×
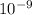`10^(-9)` / 0.530×
`10^(-3)`

sinθ = 1.02452 × [tex]10^{-3}

θ = 0.058699 degree

and

we can say

tanθ = y/D

here y is width of central maximum Y = 2y

put all value we get y

so y = D tanθ

y = 1.55 (tan0.0586)

y = 1.58528 × [tex]10^{-3} m =

so Y = 2 ( 1.58528 × [tex]10^{-3} )

so width of central maximum is 3.170566 × [tex]10^{-3} ) m