Question

A pump started filling an empty pool with water and continued at a constant rate until the pool was full. At noon the pool was 1/3 full, and 1/4 hours later it was 3/4 full. What was the total number of hours that it took the pump to fill the pool?

Answer 1

The pump fill the pool in 3/5 hours

Explanation:

From noon to 1/4 hours later, the pool goes from 1/3 to 3/4 full. That's means that the pool fill X quantity in 1/4 hours, where X is calculate as:

`X=(3)/(4) -(1)/(3)=(5)/(12)`

So, the constant rate R can be calculated as:

`R=(5/12 full )/(1/4 hours) =5/3`

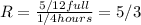
That means that every hour the pool can be fill 5/3 full, so if we want to know how many hours is needed to fill the poll one time, we can write the following equation:

`(5 full)/( 3 hours) *t = 1 full`

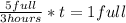
Where t is the time required to fill the pool. Solving for t we get:

t = 3/5 hours

so, the pump fill the pool in 3/5 hours or 36 minutes with a constant rate of 5/3.