Answer:
At what time will 90% of the population have heard the rumor?
The rumor was heard by 90% of the population in 5.9 hours or 5 hours and 54 minutes
So, at 1:54 pm, 90% of the population had heard the rumor.
Explanation:
To resolve this exercise we need to know the exponential model:
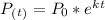 (1)
(1)
Where:
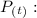 the quantity inhabitants in certain time who heard the rumor
the quantity inhabitants in certain time who heard the rumor
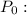 Initial people who heard the rumor
Initial people who heard the rumor
k: constant
t: time frame
We know in 4 hours (
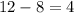 hours) half the town has heard the rumor because:
hours) half the town has heard the rumor because:
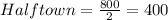 inhabitants
inhabitants
With this information we can find the constant (k), because we have all the information in
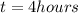
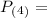 400 people
400 people
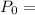 120 people
120 people
t= 4 hours
When we replace in equation 1 we have:
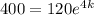
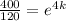

We multiply by natural logarithm on both sides of this equation and we have:
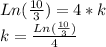
With the constant (k) we can find at what time 90% of the population have heard the rumor
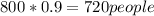 (90% of the population)
(90% of the population)
So we have:
 720 people
720 people
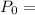 120 people
120 people
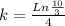
When we replace in equation 1 we have:
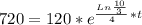
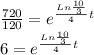
We multiply by natural logarithm on both sides of this equation and we have:
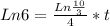

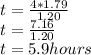
We can find how many minutes are 0.9 hours:

t= 5 hours and 54 minutes
Now, we know the rumor was heard by 90% of the population in 5.9 hours or 5 hours and 54 minutes
So, at 1:54 pm, 90% of the population had heard the rumor.