Question

A radioactive substance decays at an annual rate of 131313 percent. If the initial amount of the substance is 325325325 grams, which of the following functions fff models the remaining amount of the substance, in grams, ttt years later?

Answer 1

Answer:
`f_((t))=325(0.87)^(t)`

Step-by-step explanation:

If we have an initial amount of a radioactive material or substance, which is
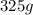`325g`, and we also are told this amount decays
`13\%` each year, this means each year
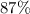`87\%` of the substance remains:

`100\%-13\%=87\%=0.87`

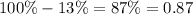
To understand it better:

Year 1:
`325(87\%)=325(0.87)`

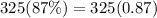
Year 2:
`325(0.87)(0.87)=325(0.87)^(2)`

Year 3:
`325(0.87)(0.87)(0.87)=325(0.87)^(3)`

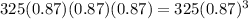
and so on until year
`t`:

Year t:
`325(0.87)^(t)`

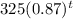
Therefore, the function tha best describes this radiation decay situation is:

`f_((t))=325(0.87)^(t)`