Question

Find the vertex, focus, directrix, and focal width of the parabola. (5 points)

negative 1 divided by 20 times x squared = y

Answer 1

`\bf \textit{vertical parabola vertex form with focus point distance} \\\\ 4p(y- k)=(x- h)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h,k+p)}\qquad \stackrel{directrix}{y=k-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{`

`\bf -\cfrac{1}{20}x^2=y\implies \cfrac{x^2}{-20}=y\implies x^2=-20y\implies (x-0)^2=-20(y-0) \\\\\\ (x-\stackrel{h}{0})^2=4(\stackrel{p}{-5})(y-\stackrel{k}{0})`

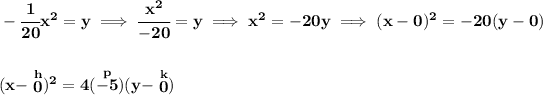
something noteworthy is that the squared variable is the "x", thus the parabola is a vertical one, the "p" value is negative, so is opening downwards, and the h,k is pretty much the origin,

vertex is at (0,0)

the focus point is "p" or 5 units down from there, namely at (0, -5)

the directrix is "p" units on the opposite direction, up, namely at y = 5

the focal width, well, |4p| is pretty much the focal width, in this case, is simply yeap, you guessed it, 20.