Answer:
Total required time is 24 minutes.
Explanation:
It is given that working together, machine J, machine K, and machine L can complete a job in 12 minutes.
Part of job completed by all machines together in one minute is
One minute work of all =
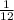
Working alone, machine J can complete a job in 20 minutes.
Part of job completed by machine J in one minute =
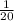
Part of job completed by machine K and L together in one minute is
One minute work of K and L together =
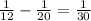
It is given that Machine J worked alone for a given amount of time. Then, machines K and L worked together, and with no other machine, for the same amount of time.
Let the given amount of time be x.
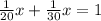
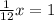
Multiply both sides by 12.
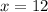
Total required time is
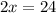
Therefore total required time is 24 minutes.