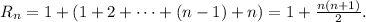Answer:
a) The recursion formula is
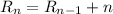 .
.
b)
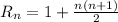 .
.
Explanation:
a) Let us explore the recurrence. A plane with only one line is divided in two regions, so
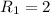 . If we add another line under the restrictions of the problem,
. If we add another line under the restrictions of the problem,
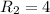 .
.
Notice that each line intersects the other n-1 lines, because there are no parallel lines. Assume we have n-1 lines and
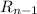 regions in the plane. If we add a new one we will have the previous
regions in the plane. If we add a new one we will have the previous
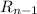 plus n new regions. Because, for each line crossed by the new one there are a new region. Therefore,
plus n new regions. Because, for each line crossed by the new one there are a new region. Therefore,
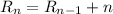 .
.
b) The method here is to develop the recurrence and find some pattern. Hence, using the formula for
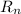 ,
,
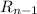 and
and
 we obtain
we obtain
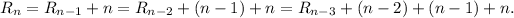
Notice that for each step back in the recurrence we add a new term in th sum. If we repeat the procedure n-1 times we will have
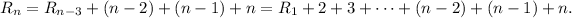
Using that
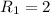 :
:

Here the smart step is to split the first 2 in 1+1, in order to obtain the sum of the first n natural numbers, and the expression for this last sum it is well known. Therefore,