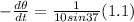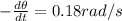Question

A ladder 10 ft long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 1.1 ft/s, how fast is the angle between the ladder and the ground changing when the bottom of the ladder is 8 ft from the wall? (That is, find the angle's rate of change when the bottom of the ladder is 8 ft from the wall.) rad/s

Answer 1

`-(d\theta)/(dt) = 0.18 rad/s`

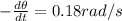
Step-by-step explanation:

As we know that the length of the ladder is given as

`L = 10 ft`

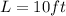
now at any instant of time let the ladder is at distance "x" from the vertical wall

then the angle made with the horizontal for the ladder is given as

`cos\theta = (x)/(L)`

now differentiate both sides with respect to time

`-sin\theta ((d\theta)/(dt)) = (1)/(L) (dx)/(dt)`

so here we have

`-(d\theta)/(dt) = (1)/(Lsin\theta)((dx)/(dt))`

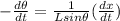
given that

`(dx)/(dt) = 1.1 ft/s`

`cos\theta = (8)/(10)`

`\theta = 37 degree`

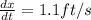
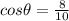
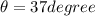
now we have

`-(d\theta)/(dt) = (1)/(10 sin37)(1.1)`

`-(d\theta)/(dt) = 0.18 rad/s`