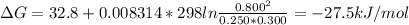Question

For a gaseous reaction, standard conditions are 298 K and a partial pressure of 1 atm for all species. For the reaction C2H6(g)+H2(g)↽−−⇀2CH4(g) the standard change in Gibbs free energy is Δ????°=−32.8 kJ/mol . What is ΔG for this reaction at 298 K when the partial pressures are ????C2H6=0.250 atm , ????H2=0.300 atm , and ????CH4=0.800 atm ?

Answer 1

ΔG = -27.5 kJ/mol

Step-by-step explanation:

The given reaction is:

`C2H6(g)+H2(g)\rightleftharpoons 2CH4(g)`

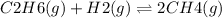
The Gibbs free energy (ΔG) is related to the standard gibbs free energy (ΔG°) as follows:

`\Delta G = \Delta G^(0)+ RTlnQ`

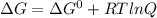
where R = gas constant

T = temperature

Q = reaction quotient

For the given reaction:

`\Delta G = \Delta G^(0)+ RTln(P(CH4)^(2))/(P(C2H6)*P(H2))`

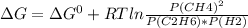
Here:

ΔG°=-32.8 kJ/mol

R = 0.008314 kJ/mol-K

T = 298 K

P(CH4) = 0.800 atm

P(C2H6) = 0.250 atm

P(H2) = 0.300 atm

`\Delta G = \-32.8+ 0.008314*298ln(0.800^(2))/(0.250*0.300)=-27.5 kJ/mol`