Answer: 7.90%
Step-by-step explanation:
Yield to maturity (YTM) measures the anticipated maximum return (interest OR i, in percentage terms) that a bond can make if it is held until it matures, and makes use of the following information:
Present value (PV) - The value presently of an amount of money as compared to its value in the future after it has been invested. This is how much it currently sells for ($1165).
Future value (FV) - The value of the amount at a specified date in the future. This is the par value (also known as face value) of the bonds ($1000).
Payment per period (PMT) - This is the systematic payments made per period and is based on the future value. In this case it is 10.2% annual payments based on the par value (therefore 10.2% x $1000)
Number of years (N) - The number of years before the asset matures. These bonds mature after 11 years.
There are various ways to calculate this figure.
Using a financial calculator (such as the HP10bII+):
1. ensure 1 period per year = 1shiftP/YR
2. Input the following in the calculator (in any order)
1000 then press FV
-1165 then press PV (this figure is negative because it is a cash outflow)
102 then press PMT
11 then press N
3. Press I/YR. This will give you 7.8999999% which can be rounded off to 7.90%
Another way to calculate this is through trial and error:
What is crucial here is identifying an interest rate. Remember YTM is always lower than the coupon rate. But that still leaves quite a lot of interest rates to go through. You can use the equation listed below to get a approximate figure for YTM:
Approximate YTM = [Annual interest payment + (par value - current price) / years to maturity] / [(current price + par value) / 2]
=
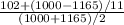
= 0.0804 or 8.04%
Another way to calculate this is by using spreadsheet