Question

A toboggan and rider have a total mass of 100 kg and travel down along the (smooth) slope defined by the equation y=0.2x2. At the instant x=8 m, the toboggan's speed is 4 m/s. At this point, determine the rate of increase in speed and the normal force which the toboggan exerts on the slope. Neglect the size of the toboggan and rider for the calculation.

Answer 1

a) Rate of increase in speed=
`a_(t)=9.361`
`m/s^(2)`

b) Normal force =
`N=310.34`
`N`

Step-by-step explanation:

Given slope=
`y=0.2*x^(2)`

Taking derivatives of both sides with respect to x,we have

`(dy/dx)=(d/dx)(0.2x^(2))`

`(dy/dx)=0.4*x`

at
`x=8`

`(dy/dx)=3.2`

`(d^(2)y/ d^(2) x)=0.4`

Where this will give us the tanΘ.

tanΘ=3.2

Θ=72.6°

Now applying equations of equilibrium in tangential direction

∑
`F_(t)=m*a_(t)`

where ∑
`F_(t)=m*g*Sin`Θ

where
`a_(t)=g*Sin`Θ

`g=9.8`
`m/s^(2)`

Rate of increase in speed=
`a_(t)=9.361`
`m/s^(2)`

Now calculate radius of curvature to figure out normal force.

`r=((1+(dy/dx)^(2))/(d^(2)y/ d^(2)x )) ^(3/2)`

Substitute values

`r=94.2`
`m`

`a_(n) =v_(n) ^(2) /r`

`v_(n)=4`
`m/s`

`a_(n)=.169`
`m/s^(2)`

∑
`F_(n)=m*a_(n)`

`N-,mgcos`Θ=
`m*a_(n)`

Normal force=
`N=310.34`
`N`

Answer 2

8.31 m/s²

567.32 N

Step-by-step explanation:

The equation is given as

y = 0.2 x²

taking derivative both side relative to "x"

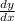`(dy)/(dx)` = 0.2 x eq-1

at x = 8 m

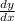`(dy)/(dx)` = 0.2 x 8 = 1.6

m = slope =
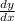`(dy)/(dx)` = 1.6

tanθ = 1.6

θ = 58 deg

Taking derivative both side relative to "x"

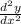`(d^(2)y)/(dx^(2))` = 0.2

Radius of curvature is given as

`r = \frac{(1 + m^(2))^{(3)/(2)}}{((d^(2)y)/(dx^(2)))}`

`r = \frac{(1 + 1.6^(2))^{(3)/(2)}}{(0.2)}`

`r = 33.6`

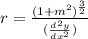
rate of increase of speed is given as

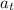`a_(t)` = g Sinθ

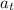`a_(t)` = (9.8) Sin58

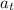`a_(t)` = 8.31 m/s²

centripetal acceleration is given as

`a_(c) = (v^(2))/(r)`

`a_(c) = (4^(2))/(33.6)`

`a_(c) = 0.48`

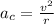
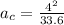
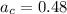
F = normal force

Force equation is given as

F - mg Cosθ = m
`a_(c)`

F - (100) (9.8) Cos58 = (100) (0.48)

F = 567.32 N