Question

A company operating under an EOQ policy enjoys rising annual demand for their products for three consecutive years. During this time their holding cost and ordering cost remain constant. Which statement is best? Their order quantity will fall but the time between orders will rise. Their order quantity will rise but the time between orders will fall. Their order quantity will rise and so will the time between orders. Their order quantity will fall and so will the time between orders.

Answer 1

Their order quantity will rise but the time between orders will fall.

Step-by-step explanation:

Let's analyse the EOQ formula:

`Q_(opt) = \sqrt{(2DS)/(H)}`

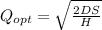
If Demand increases

The dividend increase, so the quotient increase.

EOQ will rise.

Only options b and c are correct on that statment.

Now let's check the time between order:

`(EOQ)/(Demand) * 365`

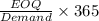
If we analyze the increase in demand:

√(2xΔDxS/H)/ ΔD

everything else is keep constant so we have:

√(CxΔD)/ ΔDx

If we use L'Hopital we can conclude this function limit is zero.

Anyway a more easy way to do it will be calculate with a demand of 1000

and then with a demand of 50,000 to notice how much the time between order decrease.

√(1000) / 1000 = 0.031622776

√(51000)/ 51000 = 0.004428074

so we have EOQ increase and days between order decrease.

Now only option B is correct !