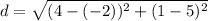Question

To the nearest tenth, what is the distance in units between the points (-2,5) and (4,1)

Answer 1

7.2 units

Explanation:

We have to use the distance formula in this.

The Distance formula says

The distance between two coordinates (a,b) and (c,d) is given by D , then

D= Sqrt { (d-b)^2+(c-a)^ }

Here

(a,b) = (-2,5)

(c,d) = ( 4,1)

Hence

D = sqrt { (5-1)^2+ ( 4-(-2))^2}

D = Sqrt { 4^2 + 6^2 }

D= Sqrt { 16+36 }

D = Sqrt 52

D= 7.211

Hence D=7.2 units

Answer 2

Answer:
`7.2\ units`

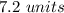
Explanation:

You need to use this formula for calculate the distance between two points:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

Given the point (-2,5) and the point (4,1), you can identify that:

`x_2=4\\x_1=-2\\\\y_2=1\\y_1=5`

Now, substituting these coordinates into the formula, you get that the distance between the given points, to the nearest tenth, is:

`d =√((4-(-2))^2+(1-5)^2)`

`d=7. 2\ units`