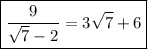Question

Question 1
Rationalise the denominator.
9
√7-2

Answer 1

`\displaystyle (9)/(√(7)-2)=3√(7)+6`

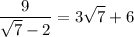
Explanation:

Rationalizing the Denominator

Rationalizing the denominator means to get rid of any radicals in the denominator.

We use the conjugate of the denominator to rationalize. The conjugate of a binomial is obtained by changing the sign that is between the two terms while keeping the same order of the terms. For example, the conjugate of

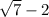`√(7)-2` is
`√(7)+2`.

We need to use the algebraic identity:

`(a-b)(a+b)=a^2-b^2`

Let's rationalize

`\displaystyle (9)/(√(7)-2)`

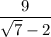
Multiply numerator and denominator by the conjugate of the denominator:

`\displaystyle (9)/(√(7)-2)=(9)/(√(7)-2)\cdot(√(7)+2)/(√(7)+2)`

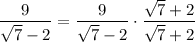
Operate in the numerator and apply the identity in the denominator

`\displaystyle (9)/(√(7)-2)=(9(√(7)+2))/((√(7)-2)(√(7)+2))`

`\displaystyle (9)/(√(7)-2)=(9√(7)+18)/((√(7))^2-2^2)`

`\displaystyle (9)/(√(7)-2)=(9√(7)+18)/(7-4)=(9√(7)+18)/(3)`

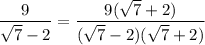
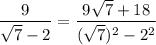
Dividing:

`\boxed{\displaystyle (9)/(√(7)-2)=3√(7)+6}`