Question

You attach a 1.10 kg block to a horizontal spring that is fixed at one end. You pull the block until the spring is stretched by 0.200 m and release it from rest. Assume the block slides on a horizontal surface with negligible friction. The block reaches a speed of zero again 0.100 s after release (for the first time after release). What is the maximum speed of the block (in m/s)?

Answer 1

6.3 m/s

Step-by-step explanation:

m = mass of the block = 1.10 kg

k = spring constant of the spring

x = stretch in the spring = 0.2 m

t = time taken by block to come to zero speed first time = 0.100 s

T = Time period of oscillation

Time period of oscillation is given as

T = 2t

T = 2 (0.1)

T = 0.2 s

Time period is also given as

`T = 2\pi \sqrt{(m)/(k)}`

`0.2 = 2(3.14) \sqrt{(1.10)/(k)}`

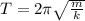
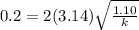
k = 1084.6 N/m

v = maximum speed of the block

using conservation of energy

Maximum kinetic energy = Maximum spring potential energy

(0.5) m v² = (0.5) k x²

m v² = k x²

(1.10) v² = (1084.6) (0.2)²

v = 6.3 m/s