Answer:
The required range is 237.5 to 275.
Explanation:
Consider the provided information.
The average cholesterol of the target population is 200 mg and they have a standard deviation of 25 mg.
The the value of μ = 200 and the
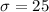
The company wished to test a sample of people who fall between 1.5 and 3 z-scores above the mean.
Let the value of z is 1.5.
Now use the z score formula:
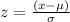
Substitute the respective values in the above formula.
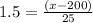
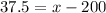
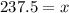
Now let the value of z is 3.
Substitute the respective values in the z score formula.
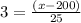

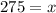
Hence, the required range is 237.5 to 275.