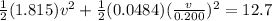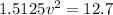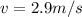Question

A hollow sphere of radius 0.200 m, with rotational inertia I = 0.0484 kg·m2 about a line through its center of mass, rolls without slipping up a surface inclined at 27.1° to the horizontal. At a certain initial position, the sphere's total kinetic energy is 20.0 J. (a) How much of this initial kinetic energy is rotational? (b) What is the speed of the center of mass of the sphere at the initial position? When the sphere has moved 0.900 m up the incline from its initial position, what are (c) its total kinetic energy and (d) the speed of its center of mass?

Answer 1

Part a)

`KE_r = 8 J`

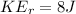
Part b)

v = 3.64 m/s

Part c)

`KE_f = 12.7 J`

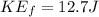
Part d)

`v = 2.9 m/s`

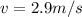
Step-by-step explanation:

As we know that moment of inertia of hollow sphere is given as

`I = (2)/(3)mR^2`

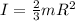
here we know that

`I = 0.0484 kg m^2`

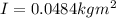
R = 0.200 m

now we have

`0.0484 = (2)/(3)m(0.200)^2`

`m = 1.815 kg`

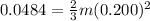
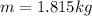
now we know that total Kinetic energy is given as

`KE = (1)/(2)mv^2 + (1)/(2)I\omega^2`

`KE = (1)/(2)mv^2 + (1)/(2)I((v)/(R))^2`

`20 = (1)/(2)(1.815)v^2 + (1)/(2)(0.0484)((v)/(0.200))^2`

`20 = 1.5125 v^2`

`v = 3.64 m/s`

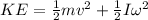
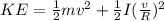
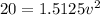
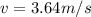
Part a)

Now initial rotational kinetic energy is given as

`KE_r = (1)/(2)I((v)/(R))^2`

`KE_r = (1)/(2)(0.0484)((3.64)/(0.200))^2`

`KE_r = 8 J`

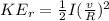
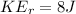
Part b)

speed of the sphere is given as

v = 3.64 m/s

Part c)

By energy conservation of the rolling sphere we can say

`mgh = (KE_i) - KE_f`

`1.815(9.8)(0.900sin27.1) = 20- KE_f`

`7.30 = 20 - KE_f`

`KE_f = 12.7 J`

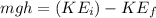
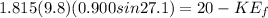
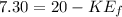
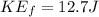
Part d)

Now we know that

`(1)/(2)mv^2 + (1)/(2)I((v)/(r))^2 = 12.7`

`(1)/(2)(1.815) v^2 + (1)/(2)(0.0484)((v)/(0.200))^2 = 12.7`

`1.5125 v^2 = 12.7`

`v = 2.9 m/s`