Question

If a polynomial is divided by x minus 5​, the quotient is 2 x squared plus 7 x minus 7 and the remainder is 7. Find the original polynomial.

Answer 1

The original polynomial is
`2x^3-3x^2-42x+42`.

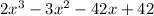Explanation:

The division of polynomial is analogue to the division of integers or natural numbers. For example, if we divide 25 by 6, we obtain that 4 is the quotient and the remainder is 1. We can recover 25 as 25 = 6*4+1.

Then, with this particular case, if we denote by P(x) the original polynomial, we have:

`P(x) = (x-5)(2x^2+7x-7)+7.`

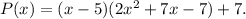
Expanding the above multiplication:

`P(x) = = 2x^3-3x^2-42x+42.`

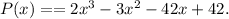
In general, given a polynomial P(x), if we divide it by another polynomial Q(x) (the divisor), there exist polynomials S(x) (the quotient) and R(x) (the remainder) such that

P(x) = Q(x)S(x) + R(x).