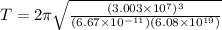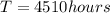Answer:
Part a)
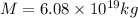
Part b)
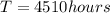
Step-by-step explanation:
As we know that stone is thrown upwards with speed
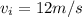
Now it returns back to the surface of Earth after t = 6 s
so the displacement of the stone is zero
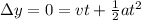
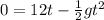
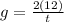
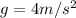
Part a)
Now we know that the circumference of the planet at the equator is of length
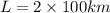
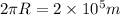
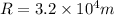
Now we have formula of acceleration due to gravity as
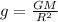
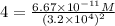
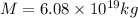
Part b)
Time to complete one revolution around the planet is given as
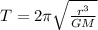
here we know that
r = distance from center of the planet
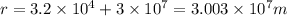
now we have