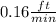Question

Gravel is being dumped from a conveyor belt at a rate of 10 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 9 ft high? (Round your answer to two decimal places.)

Answer 1

Answer: The height of the pile increasing is increasing at
`0.16(ft)/(min)`

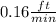
Step-by-step explanation:

Given

Rate at which gravel is being dumped ,
`\frac{\mathrm{d} V}{\mathrm{d} t}=10(ft^(3))/(min)`

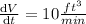
=>Rate of increase of volume of cone=
`\frac{\mathrm{d} V}{\mathrm{d} t}=10(ft^(3))/(min)`

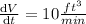
If height of the cone at any instant is h then the diameter of cone is also h

Volume of cone ,
`V=(\pi r^(2)h)/(3)=(\pi h^(3))/(4* 3)=(\pi h^(3))/(12)`

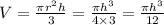
Now differentiate both sides w.r.t time(t)

`\frac{\mathrm{d} V}{\mathrm{d} t}=(\pi h^(2))/(4)\frac{\mathrm{d} h}{\mathrm{d} t}`

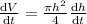
Therefore at h = 9 ft

`10=(\pi * 9^(2))/(4)* \frac{\mathrm{d} h}{\mathrm{d} t}`

=>
`\frac{\mathrm{d} h}{\mathrm{d} t}=0.16(ft)/(min)`

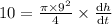
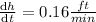
Thus the height of the pile increasing is increasing at
`0.16(ft)/(min)`