Question

A bank teller is asked to assemble $1 sets of coins for his clients. Each set is made up of three quarters, one nickel, and two dimes. The masses of the coins are quarter, 5.645 g; nickel, 4.967 g; and dime, 2.316 g. What is the maximum number of sets that can be assembled from 33.871 kg of quarters, 10.432 kg of nickels, and 7.990 kg of dimes? What is the total mass (in grams) of the assembled sets of coins?

Answer 1

1725 is the maximum number of sets that can be assembled .

45,771.15 grams is the total mass of the assembled sets of coins.

Step-by-step explanation:

Each set is made up of three quarters, one nickel, and two dimes.

3 quarters + 1 nickles + 2 dimes = 2 set

Mass of 1 quarter = 5.645 g

Number of quarters in 33.871 kg that is in 33,871 g:

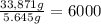`( 33,871 g)/(5.645 g)=6000` quarters

Mass of 1 nickel= 4.967 g

Number of nickles in 10.432 kg that is in 10,432 g:

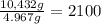`( 10,432 g)/(4.967 g)=2100` nickels

Mass of 1 dimes = 2.316 g

Number of dimes in 7.990 kg that is in 7,990 g:

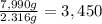`( 7,990 g)/(2.316 g)=3,450` dimes

3 quarters are in 1 set then 6000 quarters will be in:

`(1)/(3)* 6000=2000` sets

1 nickel is in 1 set then 2100 nickel will be in:

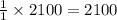`(1)/(1)* 2100=2100` sets

2 dimes are in 1 set then 3450 dimes will be in:

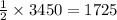`(1)/(2)* 3450=1725` sets

Since, number of dimes present are in limited number so the maximum number of set assembled will depend upon the number of dimes.

Maximum number of set assembled = 1725 sets

Total mass of assembled sets of coins

Mass of 1 set =

=3 × mass of quarter + 1 × mass of nickel + 2 × mass of dime

=3 × 5.645 g + 1 × 4.967 g+ 2 × 2.316 g =26.534 g

Mass of 1725 sets:

1725 × 26.534 g = 45,771.15 g

45,771.15 grams is the total mass of the assembled sets of coins.