Question

A shop owner has 500 cans of tomatoes that are near their expiration date.She decides to display them in a triangular pyramid and lower the price to try and sell them quickly. How many cans will be on the bottom layer, and will there be any cans left over?

Answer 1

How many cans will be on the bottom layer, and will there be any cans left over?

On the bottom layer will be 31 cans and there will be 4 cans left over

Explanation:

To resolve this problem we need to know Gauss sum of natural numbers, from k = 1 to n:

∑
`k=(n*(n+1))/(2)` (1)

We want to know the value of n when the sum is equal or close to 500, so we replace 500 in the equation (1) to find n:

`500=(n*(n+1))/(2)`

`500*2=n*(n+1)`

`1000=n^2+n`

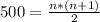
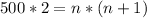
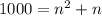
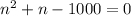`n^2+n-1000=0` (2)

We need to use the quadratic formula to resolve the equation (2)

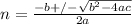`n=\frac{-b+/-\sqrt{b^(2) -4ac} }{2a}` (3)

The coefficients according to equation (2) are:

a=1

b=1

c= 1000

Now, using the quadratic formula we can find n :

Positive sign before the square root,

`n_1=\frac{-1+\sqrt{1^(2) -4(1)(-1000)} }{2(1)}`

`n_1=(-1+√(1 + 4000) )/(2)`

`n_1=(-1+63.25)/(2)`

`n_1=(62.25)/(2)`

`n_1=31.13`

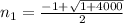
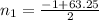
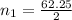
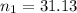
Negative sign before the square root,

`n_2=\frac{-1-\sqrt{1^(2) -4(1)(-1000)} }{2(1)}`

`n_2=(-1-√(1 + 4000) )/(2)`

`n_2=(-1-63.25)/(2)`

`n_2=(-64.25)/(2)`

`n_2=-32.13`

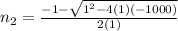
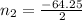
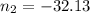
The negative term doesn't have sense in this case, We will use the positive term, the whole number closest to the answer we got when clearing n is 31, we will replace n=31 in the Gauss sum of natural numbers equation. (1)

∑
`=(n*(n+1))/(2)`

∑
`=(31*(31+1))/(2)`

∑
`=(31*(32))/(2)`

∑
`=(992)/(2)`

∑
`=496`

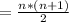
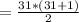
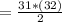
Now, we know the triangular pyramid will be 31 cans on the bottom layer and there will be 4 cans left over (500-496=4)