Answer:
(a)
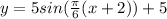
(b) 7.5ft above the low tide.
Explanation:
(a) To find the function that computes the height of the tide, you need to select the form of the sinusoidal function. For example, use the form:
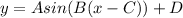
Where A is the amplitude, B the frequency, C the phase shift and D the vertical shift.
The amplitude is half the distance between the highest and the lowest tide:
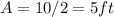
The frequency is related to the period T by:
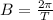
The period is 12 hours, then
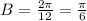
The high tide is at 1:00 a.m. and 1:00 p.m. , this is the moment when
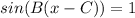 , if
, if
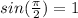 then
then
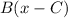 must be equal to
must be equal to
 when
when
 :
:
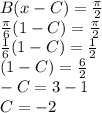
The vertical shift is the sum of the lowest value, the height of the low tide (
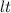 ) and the amplitude:
) and the amplitude:
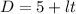
The function is:
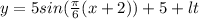
Because the function must be the height above low tide height, subtract this heigh from the function:
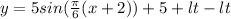
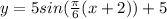
(b) Use x=11 in the function
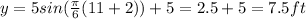 above the low tide.
above the low tide.