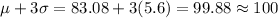Answer: 100
Explanation:
Given : The total number of seats planned in new restaurant =134
The percentage of customers demand a smoke-free area = 62%
It can also be written as

The mean of this binomial distribution will be :-
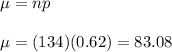
Standard deviation:-
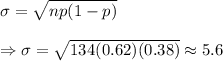
Now, the number of seats should be in the non-smoking area in order to be very sure of having enough seating there :-